Hardware Overview
Our trapped ion quantum computers are built on a chain of trapped 171Yb+ ions, spatially confined via a microfabricated surface electrode trap within a vacuum chamber. Gates are performed via a two-photon Raman transition using a pair of counter-propagating beams from a mode-locked pulsed laser. This allows for high-quality single and two-qubit transitions and all-to-all connectivity. Initialization is performed via optical pumping, and readout is performed with a combination of a resonant laser, a high numerical aperture lens, and photomultiplier tubes. A more detailed description of our current-generation hardware and its technical specifications can be found in Benchmarking an 11-qubit quantum computer (Nature Communications 10, 5464 [2019]).
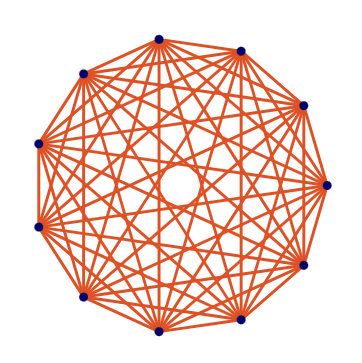
Topology
Our trapped ion QPUs are fully connected; you may run a two-qubit gate on any pair. The precise mapping of logical to physical qubits is determined at runtime to maximize performance.
Native gates
A detailed explanation of our native gates and how to use them has moved to this guide.
Calibrations
Singe-qubit gates such as the GPI and GPI2 are calibrated in two steps, first by tuning the duration and amplitude of Raman lasers to achieve the targeted bit flip, and second, by ensuring that the transition is driven on qubit resonance throughout the course of the gate, which achieves the targeted phase flip. The GZ gate is implemented by simply advancing the phase of the Raman lasers for gates that follow the GZ operation.
MS gates are calibrated by tuning the amplitude of Raman lasers to achieve the desired two-qubit rotation for each pair of qubits. An additional phase calibration is performed to maintain the same reference frame between the MS gate and the single-qubit gate per qubit to achieve the targeted MS unitary as stated above.
Best Practices
Make use of all-to-all connectivity
All-to-all connectivity between our qubits provides maximal flexibility when generating or optimizing circuits. For example, if your circuit has CX(a,b) adjacent to CX(b,a), you can replace them with a single CX gate and a SWAP gate. The swap gate can then typically be moved through the circuit and eliminated even if it increases non-locality.
Prefer RZ gates
RZ gates are performed virtually and take almost no time compared to RX and RY. If you can rotate your basis to maximize the number of rotations around the Z axis, the quality of your output should benefit. For example, when simulating the transverse-field Ising model, is better than .
Remove overly-precise gates
Rotation precision for RX and RY is about . There’s no benefit to supplying gates with angles much smaller than this.
Account for sparse return data
Only non-zero probabilities will be reported back. Keep this in mind when parsing the output.
Optimize shot counts based on expected outputs
Tailor the number of shots to the expected probability distribution of the output state and the number of gates in the circuits. Too many shots will unnecessarily increase cost. Too few shots will result in the output being indistinguishable from noise, especially for output states that have weight on many computational basis states.
Accurately account for XX gates
Arbitrary angle XX, YY and ZZ gates are not currently implemented directly in IonQ’s hardware. They are executed as two fixed-angle MS gates along with single qubit rotations.
Use consistent steps for Trotterized time-evolution
For Trotterized time-evolution, it is often easier to correct the experimental error if the same number of Trotter steps is used for every sample time, vs. if the Trotter step size is fixed and the number of steps is increased to sample at increasing times. See Fig.2 of this paper.
Use symmetry-based post-selection
A cheap way to increase the fidelity of your NISQ programs is to do symmetry-based post-selection when possible on the output probabilities. For example, if an output computational basis state is theoretically known to be not allowed but shows up anyway, discard it and re-normalize the resulting probability distribution.
Debiasing and sharpening
The previously mentioned technique (symmetry-based post-selection) was automated and available now for general public. Debiasing is the process of creating variant circuit implementations by exploiting symmetries at different levels of quantum hardware. These variations can include qubit assignments, gate decompositions, and pulse sequences. Aggregating the results of these symmetrical variants can be done through averaging or sharpening. Sharpening, implemented through plurality voting, amplifies the common results while reducing erroneous results due to hardware imperfections.
The choice between averaging and sharpening depends on the output probability distribution of the quantum algorithm. For algorithms with limited or equal probabilities among a few peaked outputs, sharpening is recommended. For algorithms with different measurement statistics, averaging should be used to avoid distortion. You can learn more about debiasing and sharpening here.