From Flash Cells to Qubits: How IonQ is Drawing Inspiration from Classical Flash Memory to Advance Quantum Error Correction

At IonQ, we are busy both delivering value to our commercial customers today and researching and developing the next-generation quantum computers of the future. Much of our research thrust is focused on the hardware and software required for error correction, which is expected to unlock even more value for customers. In collaboration with Gilles Zémor of Bordeaux University, IonQ’s quantum error correction team has proposed a novel approach to error-corrected quantum memory, inspired by classical flash memory (as detailed in this research paper). This research is part of a robust set of techniques that our quantum error correction team is exploring to reduce the overhead of quantum error correction in the long term.
This novel approach draws from classical flash memory, exploring a new paradigm called “stacked quantum memory” paired with quantum Gabidulin codes – a type of error-correcting code – to drive advancements in scalability and error correction. By leveraging lessons from classical memory systems and network coding, this research aims to address key areas in building robust quantum architectures.
The Inspiration: Classical Flash Memory
Classical flash memory cells store one or more bits of information by holding varying numbers of electrons, with the stored value determined by the cell's voltage. The manufacture of a flash cell is an incredible engineering challenge. Binary flash memory is created by charging a flash cell with either a few electrons or many electrons. In practice this is often many hundreds or thousands of electrons, but for the purposes of this diagram, we’ll use a few dozen to demonstrate the point.
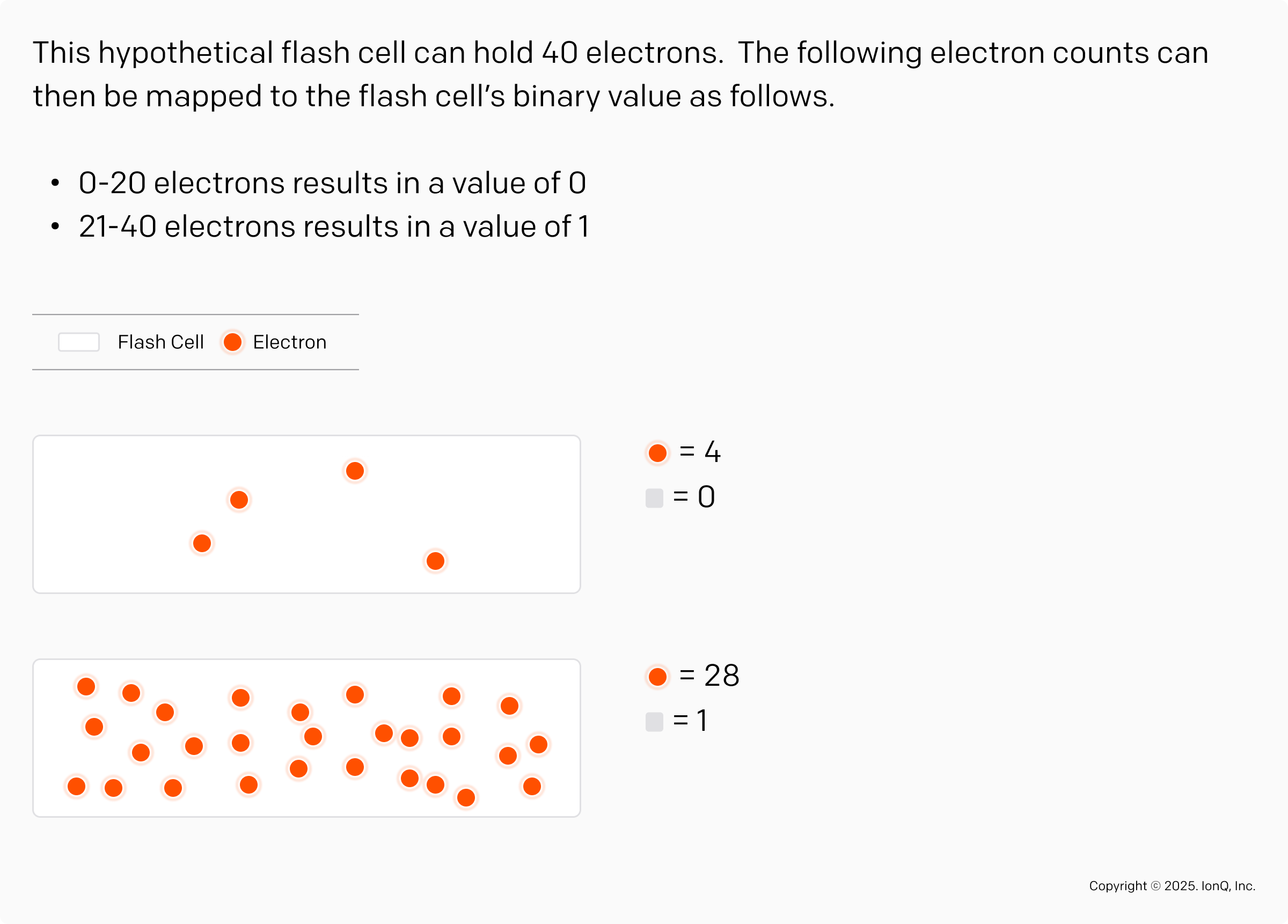
One of the key innovations for the success of flash memory is the development of the so-called multi-level flash cell, which is capable of storing multiple bits per cell.
.png)
Such a cell that stores two bits of information is called a multi-level cell. Today’s classical computing technology uses cells capable of storing three or four bits per cell and cells storing five bits per cell are currently in development.
Multi-level flash cells, capable of storing multiple bits per cell, offer advantages like higher information density and reduced manufacturing costs. Since information is more dense, it can make the memory smaller and therefore well suited to portable devices like laptops and smartphones. Second, it is more economical because fewer cells need to be manufactured. However, these cells face challenges, such as readout errors caused by wear and tear over time.
Throughout its lifetime, the value of a flash cell will change many times, which requires bringing electrons in and out of this cell. During these operations, the walls of the cell wear out, making it harder for the cell to hold its electrons. This results in a drift of the measured voltage, and therefore a readout error, when reading the value of a cell.
This issue is particularly harmful for a cell that stores multiple bits of information because it leads to errors that may affect all the bits stored. Flash memories need powerful error correction codes to deal with these errors. The lesson from the classical setting is that one may benefit from denser storage of information with multi-level cells, but only if we design an error correction protocol capable of correcting errors affecting all the bits of a cell.
Stacked Quantum Memory: Multi-Qubit Quantum Cells
Our new paper introduces a model for a stacked quantum memory inspired by classical flash memory. Our basic idea is to consider quantum cells capable of storing multiple qubits per cell.
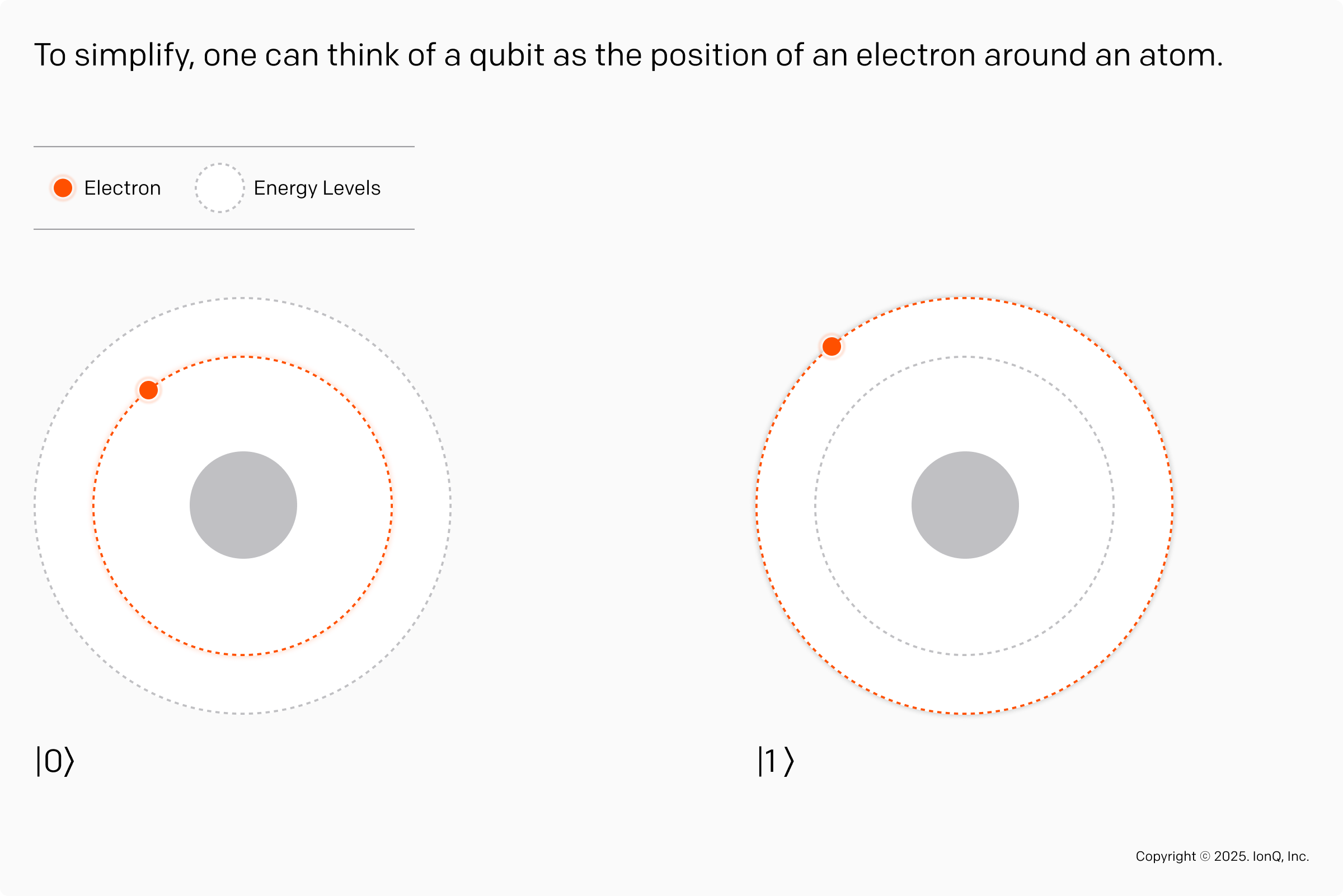
At IonQ, our cells are atoms. Each qubit is stored in an atom. Mathematically, a qubit is a superposition of the value 0 and 1 that we denote a|0⟩+b|1⟩ where a and b are complex numbers. The value |0⟩ corresponds to the electron being in the first orbit and |1⟩ corresponds to the electron being in the second orbit, like in the next figure. The electron can be in a superposition of the two orbits, allowing us to store a qubit using these two orbits.
The state of two qubits is a superposition of all possible values of two bits, that is a|00⟩+b|01⟩+c|10⟩+d|11⟩. To store two qubits in an atom, one could consider using four orbits storing two qubits as follows.
%20(1).png)
To move to three qubits per atom, we need to double again the number of orbits. A three-qubit cell is represented by a superposition of 8 orbits.
.png)
Our new paper introduces a stacked quantum memory made with cells containing multiple qubits each represented as follows.
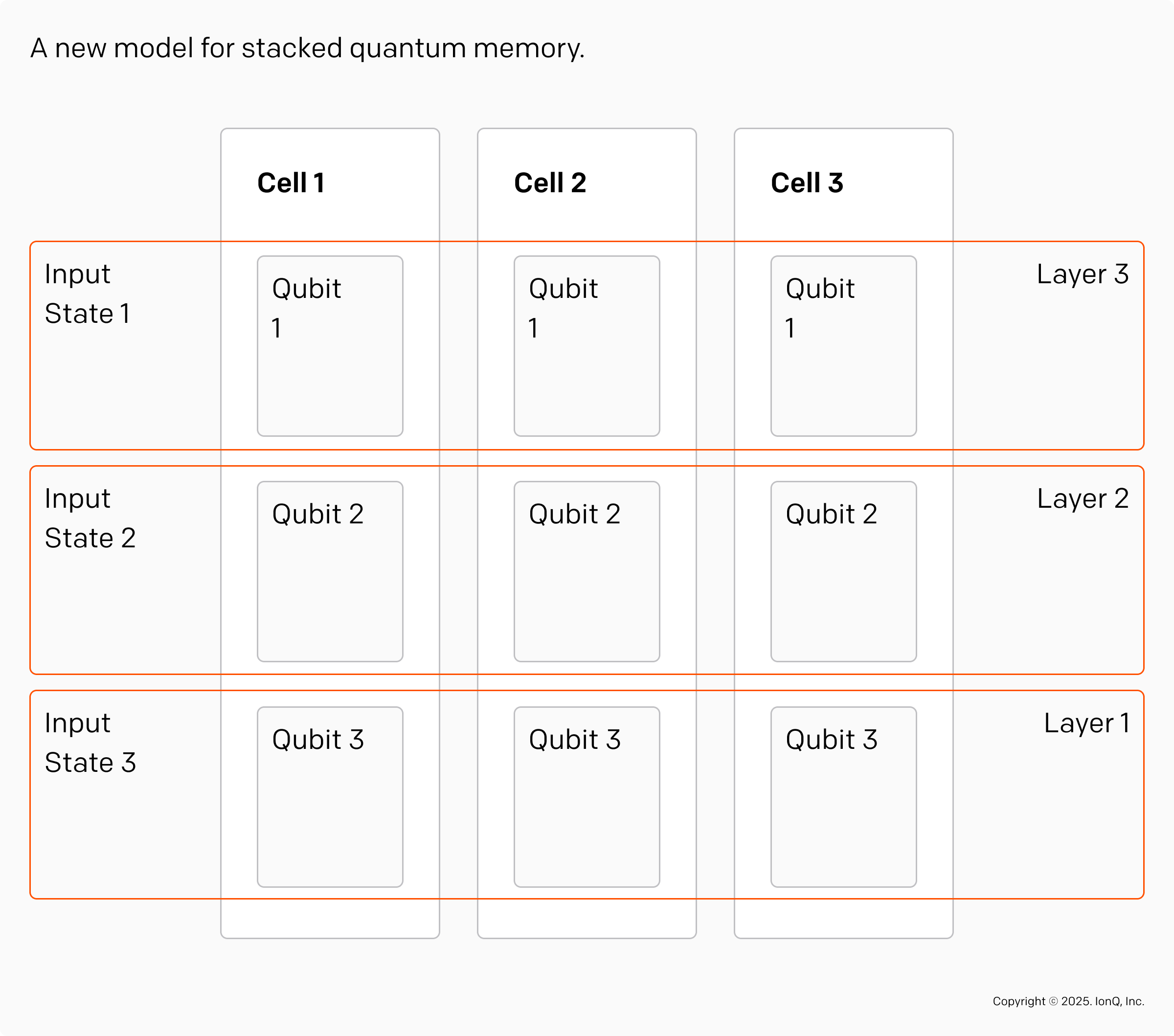
This stacked quantum memory contains three cells and each cell contains three qubits. Our new paper proposes to use stacked memories made with multi-qubit cells to increase the throughput of quantum computers as follows. Recall that a quantum computer typically works by running the same quantum circuit many times to accumulate enough statistics. Our basic idea is to run the same quantum circuit on each layer of a stacked memory. Using three-qubit cells, we would prepare an input state on each layer of the stacked memory and run the same quantum circuit three times in parallel, which could potentially lead to a 3X speed up.
Quantum Gabidulin Codes: A Promising Solution for Quantum Error Correction for Multi-Qubit Cells
With stacked quantum memory and multi-qubit cells – similar to classical flash cells – an error affecting a qubit can spread to the other qubits of the same cell. To address error propagation within multi-qubit cells, our team proposed a solution inspired by the field of classical network coding – namely, classical Gabidulin codes – to the quantum domain.
The goal of network coding is to send information through a network.
Imagine, for instance, that you are sending a text to a friend. To reach your friend, your text will travel through a network of antennas, where each antenna can send data to other antennas in its vicinity. To transmit your text, one may send data through a short path of antennas that goes from the sender (you) to the receiver (your friend). This is a good strategy for a single sender and receiver.
However, for a more complex network with many users, and where a user may want to send data to multiple receivers (think a group text for example), one can do better. A breakthrough paper from the year 2000 shows that one can send more information through the network by allowing the antennas to perform some computation on the data and to send processed data to neighboring antennas.
The following diagram illustrates the transmission of three bits through a network and the computation performed at each node of the network.
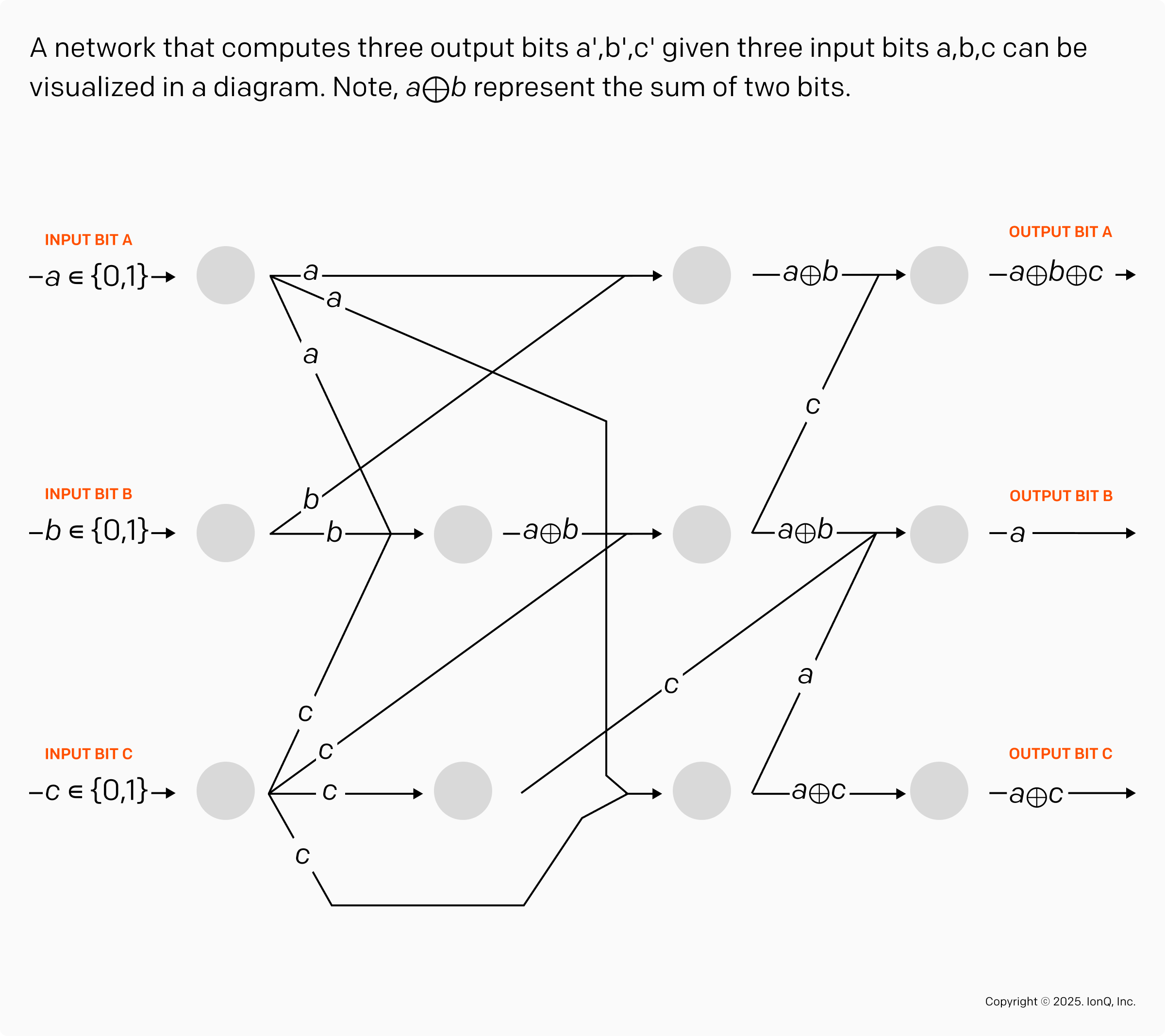
If a network contains a faulty edge, the result sent through this edge may be incorrect. If left uncorrected, this type of fault is very harmful because it can rapidly spread to other nodes, as we see below:
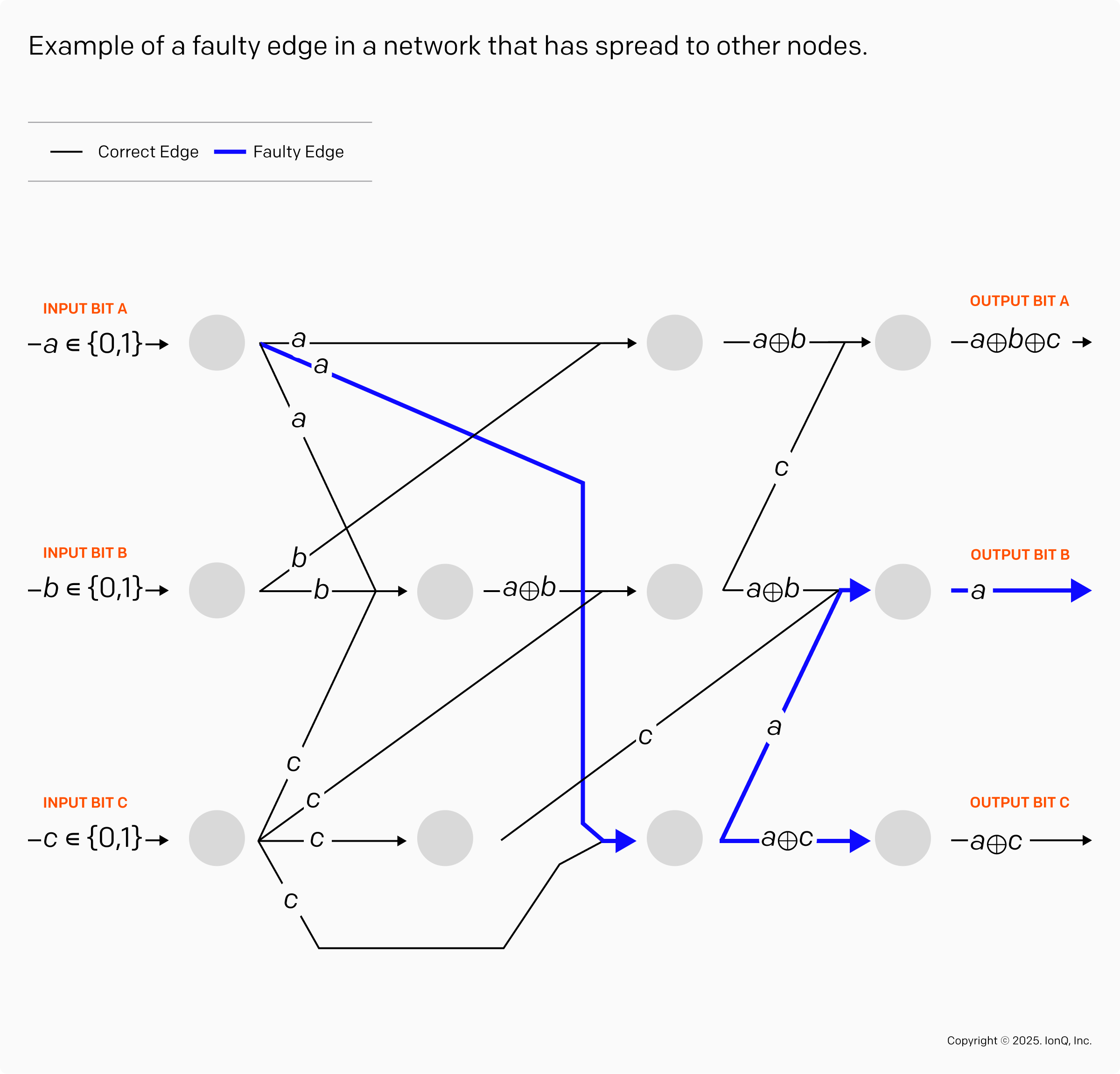
A single faulty edge may spread to two output bits as we can see on the blue path in the previous figure. This phenomenon is analogous to a fault in a qubit that spreads to the other qubits during a quantum computation.
Exploiting this resemblance, we design a quantum version of Gabidulin codes, which are used to correct faults in classical networks, and demonstrate that they can be used to correct faults in stacked quantum memory. The detailed construction of quantum Gabidulin code is too technical for this post but we invite the reader to check our paper for more information.
Key Takeaways: A Potential Long-Term Approach to Error Correction and Scale
Our proposed solution has many key benefits that make it a potential viable longer-term approach to advancing error correction, namely:
- New approach to fault tolerance and smarter error correction: Treating circuit faults as low-rank matrices, allowing for new quantum error correction schemes, potentially more qubit-efficient than standard methods.
- Increased throughput and faster processing: Designing stacked memory capable of running key quantum operations (Clifford circuits) on multiple inputs simultaneously, potentially increasing the throughput of future systems.
- Real-world applications and impact: Could accelerate variational quantum algorithms (e.g. optimization applications) and generate key quantum resources for fault-tolerant computing.
While important milestones remain, our discoveries in this work mark a major leap forward in tackling two of quantum computing’s biggest areas of focus: scalability and error correction. Inspired by classical flash memory and powered by advanced quantum error correction, our approach has the potential to enable denser, more reliable quantum memory systems—paving the way for practical, large-scale quantum architectures. Though still in early stages, this work is actively shaping the foundation for next-generation quantum systems. We see a clear path forward and invite collaboration to accelerate the real-world impact of quantum technologies sooner than expected.

