Today, the IonQ team is excited to announce that IonQ Aria, our latest quantum computer, has achieved a record 20 algorithmic qubits (#AQ), furthering its lead as the most powerful quantum computer in the industry. In other words, IonQ Aria is able to run hundreds of accurate quantum gates in a single algorithm, whereas previous quantum computers were only capable of running dozens of gates at a time. This is a momentous day for IonQ and the quantum computing industry, and we hope you’ll read on to learn more about the accomplishment and underlying data.
Followers of the quantum computing industry understand that qubit count alone is not enough to understand a quantum computer’s performance, even if the industry hasn’t reached consensus on an alternative. So why is it still the first question everyone asks when comparing quantum computers?
One explanation is that quantum computing is a rapidly-advancing but still-nascent industry. Even though more and more people are beginning to understand quantum computing, most haven’t had the time to learn the nuances of how to measure and understand progress. Adoption of new technology takes time.
The main reason the industry resorts to qubit count is that it's a single number, making it easy to understand. Single numbers are easier to compare than a table of detailed specs, even if that one number doesn’t capture the full complexity of a computer’s performance.
This post will explore the rationale for why a single metric is important and our work on defining and refining our preferred single-number metric for quantum computing—algorithmic qubits (#AQ). We believe that a well crafted metric for quantum computing is necessary for both solution providers and customers and that it can evolve over time to accommodate the changing needs. In this post, we will cover the technical definition of #AQ as well as the performance of IonQ Aria, our latest quantum computer, which has achieved an industry-leading #AQ of 20!
But, before we get into the technical details, let’s start by talking about why single-number metrics are so hard to define and use in the first place.
A Superior Single-Number Metric: Algorithmic Qubits
The benefits of only having one number are straightforward: one number is easier to compare, share, and read. But there are also several drawbacks to single-number metrics.
The first is that one number can’t capture every nuance1 , so significant efforts are made to capture as much information in a single-number metric as possible to make it more descriptive. Think about numbers that summarize a lot of information to speak for a broader context, such as GDP for economists or an overall score for a figure skater. Today, we’re missing a good single-number metric for quantum computing.
Another limitation of single-number metrics is that they assume everyone wants to know the same information. An economist might care about a country’s GDP, but an environmental scientist might concern herself more with the country’s carbon footprint. Different people and organizations value different things, so not every single-number metric will be ideal for every audience.
A good single-number metric is one that represents the needs of the people using what it’s measuring. It simplifies and clarifies by focusing on the utility or value that users seek.
So, what would be a good candidate for a single-number metric in quantum computing during these early days of development?
The most important thing for a single-number metric to communicate is what a given quantum computer can do for its end users. After all, when we are talking to customers, investors, and the public, the question we get most is not, “what are the specs?”, it’s “what can it do?”. Instead of being concerned with individual features like gates, connectivity, error rates and qubits, a good single-number metric for quantum computers should indicate how good the entire system is at solving problems. That means running basic algorithms that will be the building blocks for solving real-world problems, which we call “algorithmic qubits” (#AQ for short).
An algorithmically-focused metric will not be right for everyone and every context. A user-oriented metric focused on applications is the most useful in bringing quantum computers out of the lab and into the market. Other, more localized performance metrics will still offer additional value for more complete understanding and deeper analysis.
In the past, we have roughly defined an #AQ of N as the size of the largest circuit you can successfully accomplish with N qubits and N² two-qubit gates. Here, we bring additional thoughts on how to define it, and rigor in terms of how one should measure it.
A Rigorous Definition
Providing a precise and rigorous definition for #AQ does two critical things: it creates a replicable metric for people who want to test our hardware or anyone else’s, and just as importantly, it keeps us honest. The goal is to define a standard metric that the entire industry can use, which can only be achieved by scrutinizing any loopholes and converging to a solution through open debate. A rigorous and replicable definition achieved through such a process will serve as an effective means to accommodate communication between the builders and the users of quantum computers. This will help expand both the utility of quantum computers and the trust between providers and customers in the industry.
It’s worth calling out that in the process of calculating #AQ for any given computer, the user will gain insights into the specific performance of that computer across a broad variety of real-world algorithms. This second-level data can and should be used to offer additional insights that might inform customer decisions, and should be provided with clarity.
We plan to continue collaborating with customers, partners and industry peers, ideally through a relevant standards body, to build the most legible, meaningful metric we can in #AQ. At the same time, we recognize that it won’t be perfect, especially not at first. And, as a single-number metric, it will have inherent limitations. IonQ is committed to helping customers and curious early adopters understand this technology as best we can, and shaping as best a single-number metric as we can is a useful step along that journey.
Measuring What Matters and Ignoring Randomness
To understand how “good” a computer is at computing, we typically look at two factors: the space of all problems that the computer can in principle tackle, and the relevant subspace where useful problems reside.
To illustrate this point, let’s use an example that is closer to our lives: streaming high-definition (HD) video through our home Internet. The 1080p video format has about 2.07 million pixels, each with 24 bits. With this many bits, in order to transmit at 60 frames per second, we would need to handle 2.98Gbps2 . Most homes don’t have this type of internet bandwidth, but within the total space of 249680000 possible images you could theoretically compose in this video format, the relevant subspace of images that would be meaningful to humans is only a very small fraction. Streaming companies leverage this relevant subspace to develop a highly efficient compression algorithm for this problem that requires 600 times less bandwidth!
This observation about relevant subspaces is true for quantum computation as well: like the subspace of images in a video, useful quantum algorithms will likely have a relevant subspace of meaningful output states. This is in contrast to circuits that serve the purpose of proving quantum supremacy in which the lack of structure in the output is a desirable property. We are motivated to drive our technology forward in a productive and useful direction and therefore emphasize that #AQ should be tailored to evaluating useful quantum algorithms, rather than spending too much effort benchmarking algorithms that produce quantum states that look like the output of random circuits.
Quantum Volume (QV) and cross-entropy benchmarking used in quantum supremacy experiments were developed to characterize a quantum computer’s ability to perform random circuits. While there is some value to such an approach in probing the fundamental limits of quantum computation, it pays unnecessary amounts of attention to the “irrelevant subspace” or randomness and fails to focus on the relevant subspace where most of the useful and practical quantum algorithms are expected to reside.
Our formal definition of algorithmic qubits (provided below), while embracing the foundational notion of running ~N² entangling gates over N qubits, moves away from any attention to random circuits and focuses on structured quantum circuits that are of practical relevance. Therefore, #AQ as defined has no formal relationship to metrics like QV that are based on random circuits. Instead, we propose a wide range of practical quantum algorithms that are of interest to the industry, as outlined in the pioneering work led by the Quantum Economic Development Consortium (QED-C). Given that new applications and underlying algorithms will continue to evolve, we adopt a mechanism by which additional measurements are introduced regularly so the metric can evolve with the industry. This is in line with modern benchmarking approaches for classical high-performance computers, such as the SPEC benchmarks.
The Definition of Algorithmic Qubits (#AQ)
In defining the #AQ metric, we derive significant inspiration from the recent benchmarking study from the QED-C. Just like the study, we start by defining benchmarks based on instances of several currently popular quantum algorithms. Building upon previous work on volumetric benchmarking, we then represent the success probability of the circuits corresponding to these algorithms as colored circles placed on a 2D plot whose axes are the ‘depth’ and the ‘width’ of the circuit corresponding to the algorithm instance.
The expression #AQ = N, can then be defined as a side of the largest box of width N and depth N² that can be drawn on this volumetric background, such that every circuit within this box meets the success criteria. Note that here we will change the definition of depth and success criteria from that of the QED-C work to be more relevant to near-term quantum computers.
The set of algorithms that are relevant to users will change over time as quantum computers become more powerful and we gain a better understanding of the market needs. The benchmarking suite should include a representative subset of these algorithms. For version 1.0, we have chosen algorithm implementations from the QED-C repository. The algorithms chosen span a variety of circuit widths and depths. We exclude algorithms that can be reduced to circuits that include no entanglement such as Bernstein-Vazirani.
New benchmarking suites should be released regularly, and be identified with an #AQ version number. The #AQ for a particular quantum computer should reference this version number under which the #AQ was evaluated. Ideally, new versions should lead to #AQ values that are consistent with the existing set of benchmarks and not deviate drastically, but new benchmarks will cause differences, and that is the intention - representing the changing needs of customers.
Various types of optimizations are going to greatly affect the performance experienced by users of quantum computers, similar to the impact of optimizations in classical benchmarking (as discussed for instance in Section 1.4 of the SPEC rules for HPC system). We do not have enough experience with quantum optimizers yet to draw up an exhaustive list of what should and should not be allowed. So today, we start with a relatively simple set of rules, with the understanding that these rules will evolve over time to make sure that the application-based benchmarking remains a highly relevant metric with which developers and users of quantum computers communicate effectively.
For those who are interested in the set of rules that rigorously define #AQ Version 1.0, they can be found below. We also provide a repository containing the rules and benchmark algorithms on GitHub. The current version of the repository contains code in Qiskit which allows one to measure #AQ when executed on a quantum backend. Instructions to run the code are in the file AQ.md.
Rules For #AQ Version 1.0:
This repository defines circuits corresponding to instances of several quantum algorithms. The AQ.md document in the repository outlines the algorithms that must be run to calculate #AQ.
The circuits are compiled to a basis of CX, Rx, Ry, Rz to count the number of CX gates. For version 1.0, the transpiler in Qiskit version 0.34.2 must be used with these basis gates, with the seed_transpiler option set to 0, and no other options set.
A circuit can be submitted before or after the above compilation to a quantum computer. By quantum computer, here we refer to the entire quantum computing stack including software that turns high-level gates into native gates and software that implements error mitigation or detection.
If the same algorithm instance can be implemented in more than one way using different numbers of ancilla qubits, those must be considered as separate circuits for the purposes of benchmarking. A given version of the repository will specify the implementation and number of qubits for the algorithm instance.
If the oracle uses qubits that return to the same state as at the beginning of the computation (such as ancilla qubits), these qubits must be traced out before computing the success metric.
Any further optimization is allowed as long as (a) the circuit to be executed on QC implements the same unitary operator as submitted, and (b) the optimizer does not target any specific benchmark circuit.
These optimizations may reduce the depth of the circuit that is actually executed. Since benchmarking is ultimately for the whole quantum computing system, this is acceptable. However, the final depth of the executed circuit (the number and description of entangling gate operations) must be explicitly provided.
Provision (b) will prevent the optimizer from turning on a special purpose module solely for the particular benchmark, thus preventing gaming of the benchmark to a certain extent.
Error mitigation techniques like randomized compilation and post-processing have to be reported if they are used. Post-processing techniques may not use knowledge of the output distribution over computational basis states.
The success of each circuit run on the quantum computer is measured by the classical fidelity defined against the ideal output probability distribution:
where is the ideal output probability distribution expected from the circuit without any errors and is the measured output probability from the quantum computer, and represents each output result.
The definition of #AQ is as follows:
Let the set of circuits in the benchmark suite be denoted by.
Locate each circuit as a point on the plot by its
Width, = Number of qubits, and
Depth, = Number of CX gates
Define success probability for a circuit :
Circuit passes if , where is the statistical error based on the number of shots, where is the number of shots, and is the threshold.
Then, define #AQ=, when
The data should be presented as a volumetric plot. The code to plot this is provided in
An additional accompanying table should list for each circuit in the benchmark suite the number of qubits, the number of each class of native gates used to execute the circuit, the number of repetitions of each circuit in order to calculate , and for each circuit.
#AQ Measurement for IonQ’s Latest Quantum Computer
As announced in our latest press release , we recently completed the testing of our latest quantum computer, IonQ Aria. In preparation for this blog post, and in accordance with the process described above, we measured the performance of operating these benchmark algorithms on this new computer and are proud to report the results.
In the spirit of this benchmarking effort and in full compliance with the rules that we set for ourselves, it is important to always offer transparency and clarity about what’s being measured and reported. We include a table of critical circuit features executed to generate this plot.
We applied advanced error mitigation techniques at the circuit execution level that improve the success probability of algorithm execution. One of the most widely-adopted error mitigation strategies is to utilize the symmetry in the quantum circuit execution, and look for the presence of errors by monitoring the resulting symmetry after the computation is completed. Because these symmetries do not require the knowledge of the final answer, they can be deployed generally to arbitrary quantum algorithms and are designed into our computer’s standard execution layer. The key symmetry we utilized is our ability to map the quantum circuit to different qubits and gates in our system: the results of the quantum computation based on these diverse mappings are consolidated to mitigate errors at the execution layer. This approach is referred to as debiasing via frugal symmetrization, or just debiasing, by the IonQ team. A preprint about the technique can be found on the arXiv here. It has also been referred to as exploiting state-dependent bias, diverse mapping, and error-aware mapping in previous research (Ref1, Ref2, Ref3). Debiasing is a default part of algorithm execution for IonQ Aria.

The above figure shows the measurement results for the various benchmark algorithms on IonQ Aria. The vertical and horizontal axis represents the number of qubits and the number of entangled gates used in each algorithm provided in the repository, respectively. Each circle therefore corresponds to an executed algorithm, and the color indicates the resulting fidelity (success probability). The gray rectangle is drawn up to N qubits and N2 entangling gates, such that all circles in it achieves fidelity of over 37%, The measured #AQ is 20 in this case, which means one can execute a quantum circuit over 20 qubits that contain about 400 entangling gate operations and expect the results to be correct with confidence of 37% or higher.
The full dataset can be found here.
#AQ vs. QED-C’s Proposed Benchmark
The definition of #AQ is inspired by the work on application-oriented performance benchmarks led by the QED-C Technical Advisory Committee (TAC) on Standards and Performance Benchmarks. The Committee’s work established the framework for measuring the performance of a quantum computer based on a set of algorithms, and adopted a volumetric plot to display the results. The definition of #AQ is a simple extension of extracting a single-number metric from this framework.
However, there are two changes that are introduced from the definitions adopted by QED-C TAC.
First is the definition of circuit depth, which defines the horizontal axis in the plot for the data. In QED-C TAC work, the circuit depth is defined to include both single and two qubit gates. In the #AQ definition, we only track the number of two-qubit gates in the circuit to simplify the definition. Given that single qubit gates are more accurate in most quantum computer hardware, this would provide a more representative performance for other algorithms with similar structures as those adopted in the metric.
Second is the definition of success criteria for each algorithm included in the benchmark. Since the QED-C effort did not include an attempt to define a numerical metric, there was no explicit definition of the success criteria based on a threshold of the resulting fidelity. We adopted a fidelity metric different from that used in the QED-C work, and have introduced a success criteria based on evaluation of this fidelity.
For the purpose of comparison, the following plots show the performance of IonQ Aria against the QED-C benchmarks after the error mitigation steps are applied. We note that the data plotted in this figure is identical to that used to extract the #AQ metric, but the noted differences are reflected (definition of horizontal axis and the computation of the fidelity shown in color). To further help with this comparison, we plotted the performance of the QED-C benchmarks measured in other quantum computers available through public access through their standard interface.
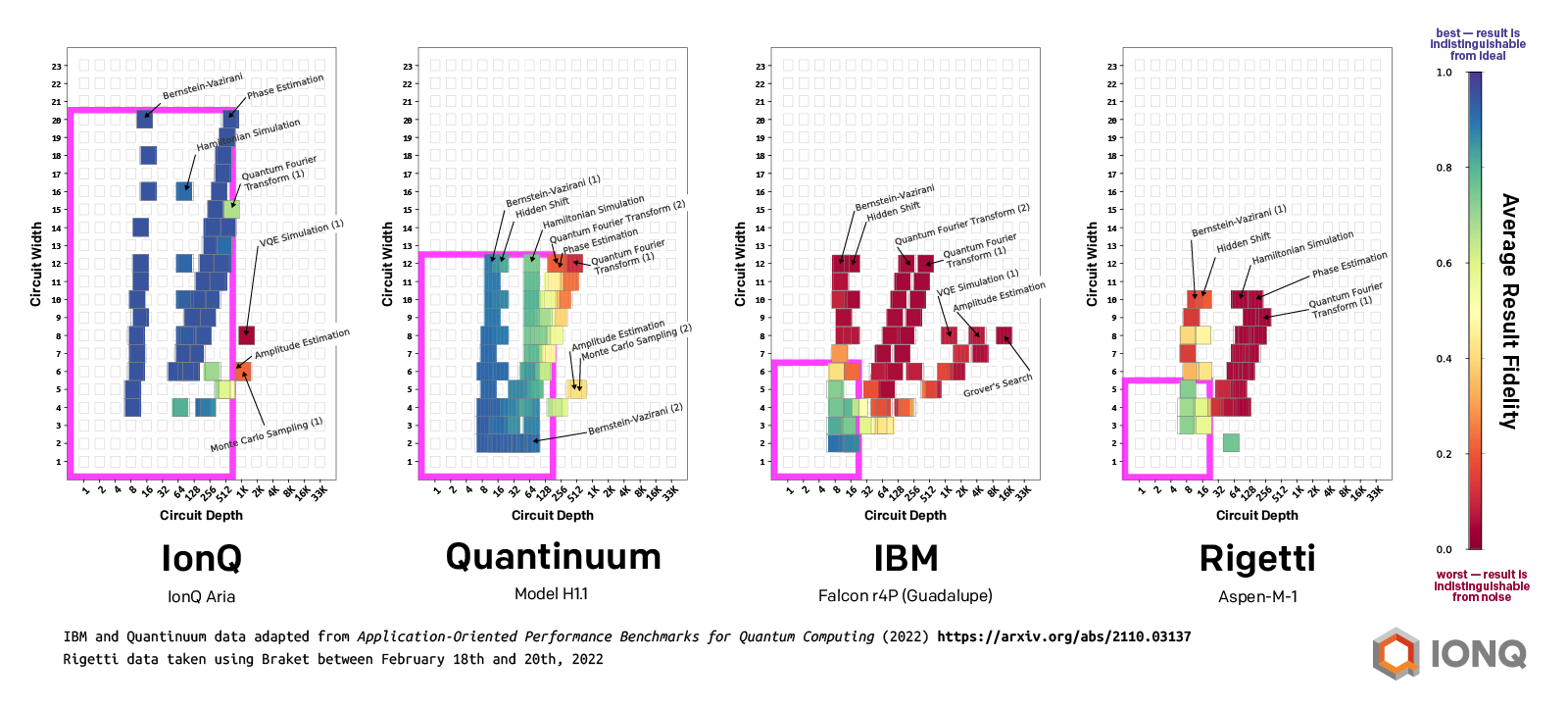
Side-by-side comparison of quantum computers using QED-C benchmarks. The vertical and horizontal axis represents the number of qubits (circuit width) and the number of quantum gates (circuit depth) used in each algorithm provided in the repository, respectively. Each square corresponds to an executed algorithm, and the color indicates the resulting fidelity (polarization fidelity in this case). Pink rectangles indicate the range in which algorithms are likely to succeed. Data for IBM and Quantinuum adapted from Application-Oriented Performance Benchmarks for Quantum Computing, data for Rigetti taken using Braket between Feb 18-20, 2022.
Help Us Make #AQ Better
Although this is the end of this post, it’s just the beginning of the conversation. IonQ is committed to furthering collaboration in the quantum computing industry and to maintaining focus on performance metrics that facilitate effective communication between builders and users of quantum computers. We are spending a significant amount of time thinking and investing in metrics that would be helpful and facilitate sorely needed transparency about quantum computers and their actual utility. From common useful metrics with clear definitions to a single-metric benchmark for capturing utility, and a consistent measurement of the performance of individual algorithms, as described in this blog post.
We welcome your thoughts and future contributions. Email us at [email protected].
1 Even in mature industries like semiconductors, a similar set of challenges emerge. See: https://spectrum.ieee.org/a-better-way-to-measure-progress-in-semiconductors ↫
2 24 bits/pixel x 60 frames/sec x 2.07Mpixels/frame = 2.98 Gigabits per second↫